Simple Cipher Encryption Key Generator
Nov 04, 2014 Meet Eddie Woo, the maths teacher you wish you’d had in high school Australian Story - Duration: 28:09. ABC News In-depth Recommended for you. Usage Guide - RSA Encryption and Decryption Online. In the first section of this tool, you can generate public or private keys. To do so, select the RSA key size among 515, 1024, 2048 and 4096 bit click on the button. Caesar cipher: Encode and decode online. Method in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. The method is named after Julius Caesar, who used it in his private correspondence. URL encode Text to morse code Affine cipher Hex to Base32.
- Cryptography Tutorial
However, many applications that use RC4 simply concatenate key and nonce; RC4's weak key schedule then gives rise to related key attacks, like the Fluhrer, Mantin and Shamir attack (which is famous for breaking the WEP standard). Because RC4 is a stream cipher, it is more malleable than common block ciphers.
- Cryptography Useful Resources
- Selected Reading
The Data Encryption Standard (DES) is a symmetric-key block cipher published by the National Institute of Standards and Technology (NIST).
DES is an implementation of a Feistel Cipher. It uses 16 round Feistel structure. The block size is 64-bit. Though, key length is 64-bit, DES has an effective key length of 56 bits, since 8 of the 64 bits of the key are not used by the encryption algorithm (function as check bits only). General Structure of DES is depicted in the following illustration −
/last-fm-generate-api-key.html. Since DES is based on the Feistel Cipher, all that is required to specify DES is −
- Round function
- Key schedule
- Any additional processing − Initial and final permutation
Initial and Final Permutation
The initial and final permutations are straight Permutation boxes (P-boxes) that are inverses of each other. They have no cryptography significance in DES. The initial and final permutations are shown as follows −
Round Function
The heart of this cipher is the DES function, f. The DES function applies a 48-bit key to the rightmost 32 bits to produce a 32-bit output.
Expansion Permutation Box − Since right input is 32-bit and round key is a 48-bit, we first need to expand right input to 48 bits. Permutation logic is graphically depicted in the following illustration −
The graphically depicted permutation logic is generally described as table in DES specification illustrated as shown −
XOR (Whitener). − After the expansion permutation, DES does XOR operation on the expanded right section and the round key. The round key is used only in this operation.
Substitution Boxes. − The S-boxes carry out the real mixing (confusion). DES uses 8 S-boxes, each with a 6-bit input and a 4-bit output. Refer the following illustration −
The S-box rule is illustrated below −
There are a total of eight S-box tables. The output of all eight s-boxes is then combined in to 32 bit section.
Straight Permutation − The 32 bit output of S-boxes is then subjected to the straight permutation with rule shown in the following illustration:
Key Generation
The round-key generator creates sixteen 48-bit keys out of a 56-bit cipher key. The process of key generation is depicted in the following illustration −
The logic for Parity drop, shifting, and Compression P-box is given in the DES description.
DES Analysis
The DES satisfies both the desired properties of block cipher. These two properties make cipher very strong.
Avalanche effect − A small change in plaintext results in the very great change in the ciphertext.
Completeness − Each bit of ciphertext depends on many bits of plaintext.
Simple Cipher Encryption Key Generator Software
During the last few years, cryptanalysis have found some weaknesses in DES when key selected are weak keys. These keys shall be avoided.
DES has proved to be a very well designed block cipher. There have been no significant cryptanalytic attacks on DES other than exhaustive key search.
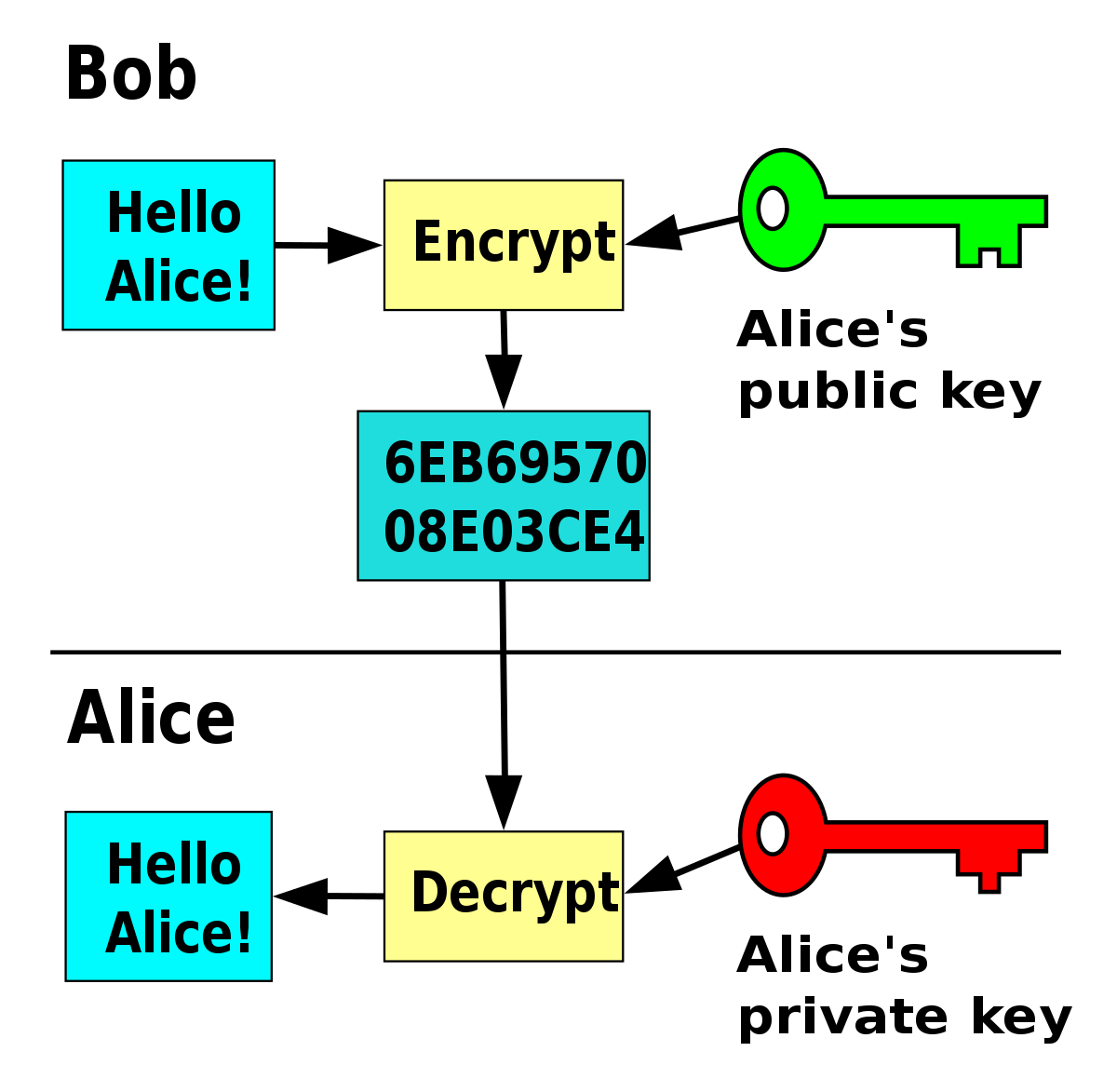
-->Creating and managing keys is an important part of the cryptographic process. Symmetric algorithms require the creation of a key and an initialization vector (IV). The key must be kept secret from anyone who should not decrypt your data. The IV does not have to be secret, but should be changed for each session. Asymmetric algorithms require the creation of a public key and a private key. The public key can be made public to anyone, while the private key must known only by the party who will decrypt the data encrypted with the public key. This section describes how to generate and manage keys for both symmetric and asymmetric algorithms.
Symmetric Keys
The symmetric encryption classes supplied by the .NET Framework require a key and a new initialization vector (IV) to encrypt and decrypt data. Whenever you create a new instance of one of the managed symmetric cryptographic classes using the parameterless constructor, a new key and IV are automatically created. Anyone that you allow to decrypt your data must possess the same key and IV and use the same algorithm. Generally, a new key and IV should be created for every session, and neither the key nor IV should be stored for use in a later session.
To communicate a symmetric key and IV to a remote party, you would usually encrypt the symmetric key by using asymmetric encryption. Sending the key across an insecure network without encrypting it is unsafe, because anyone who intercepts the key and IV can then decrypt your data. For more information about exchanging data by using encryption, see Creating a Cryptographic Scheme.
The following example shows the creation of a new instance of the TripleDESCryptoServiceProvider class that implements the TripleDES algorithm.
When the previous code is executed, a new key and IV are generated and placed in the Key and IV properties, respectively.
Sometimes you might need to generate multiple keys. In this situation, you can create a new instance of a class that implements a symmetric algorithm and then create a new key and IV by calling the GenerateKey and GenerateIV methods. The following code example illustrates how to create new keys and IVs after a new instance of the symmetric cryptographic class has been made.
When the previous code is executed, a key and IV are generated when the new instance of TripleDESCryptoServiceProvider is made. Another key and IV are created when the GenerateKey and GenerateIV methods are called.
Asymmetric Keys
The .NET Framework provides the RSACryptoServiceProvider and DSACryptoServiceProvider classes for asymmetric encryption. These classes create a public/private key pair when you use the parameterless constructor to create a new instance. Asymmetric keys can be either stored for use in multiple sessions or generated for one session only. While the public key can be made generally available, the private key should be closely guarded.
A public/private key pair is generated whenever a new instance of an asymmetric algorithm class is created. After a new instance of the class is created, the key information can be extracted using one of two methods:
List Of Encryption Ciphers
The ToXmlString method, which returns an XML representation of the key information.
The ExportParameters method, which returns an RSAParameters structure that holds the key information.
/windows-xp-pro-sp3-serial-key-generator.html. Both methods accept a Boolean value that indicates whether to return only the public key information or to return both the public-key and the private-key information. An RSACryptoServiceProvider class can be initialized to the value of an RSAParameters structure by using the ImportParameters method.
Asymmetric private keys should never be stored verbatim or in plain text on the local computer. If you need to store a private key, you should use a key container. For more on how to store a private key in a key container, see How to: Store Asymmetric Keys in a Key Container.
The following code example creates a new instance of the RSACryptoServiceProvider class, creating a public/private key pair, and saves the public key information to an RSAParameters structure.